Your cart is currently empty!

Thirty Years with David Bohm
the December 2020 issue of Pari Perspectives.
It is an honor to be invited to pay tribute to David Bohm with whom I had the privilege to work with for over thirty years at Birkbeck College, University of London. We started on the same day and spent the rest of our careers at the same institution. We had many discussions over the years on a set of wide-ranging topics, both inside and outside of physics. Here I will concentrate on the development of Bohm’s ideas about quantum phenomena, leaving the wider implications of these ideas to those at the meeting who are in a far better position to discuss them.
Introduction
I was extremely happy to be invited to pay a tribute to David Bohm in the centenary year of his birth. Visiting Pari is always a pleasure. The people are so welcoming; the food is a delight. I wish I had more time to spend here with the wonderful people of Pari.
Let me start at the beginning. I first met David in 1961 on a fine sunny spring weekend at Cumberland Lodge in Great Windsor Park. My PhD with Cyril Domb, Mike Fisher and Martin Sykes was coming to an end. I had had a lot of fun working on the Ising model and applying some of the techniques to ferromagnets and the protein folding problem, but the time had come to move on to pastures new.
The Lodge was set up by Amy Buller as an institute where students could meet to explore the moral issues of the day and ‘to provide a safe space for “unsafe” discussions and to foster learning and critical thinking.’ This was an admirable venue to invite David Bohm to—to present his ideas on the meaning of quantum theory.
The atmosphere in the physics community at that time was one of total opposition, nay open hostility, to any proposals for an ontology that might underlie quantum mechanics, particularly when the words ‘hidden variables’ were mentioned. Bohr and Einstein had battled it out in 1935 and Bohr was perceived to be the victor. ‘There is only one interpretation possible’ were the words that Peierls used in a letter responding to a paper I was trying to get published. So, in the eyes of the orthodoxy of the day, Bohm was a heretic.
But why was he a heretic? All he had done was to split the Schrödinger equation into its real and imaginary parts under polar decomposition of the wave function, a process that sixth form students are taught to do1. The form of the resulting equations suggested an interpretation that did not fit in to the orthodoxy. However, if we read Dirac’s classic Quantum Mechanics carefully we find Dirac himself starting on the road Bohm later trod, but gave up because he felt it violated the Heisenberg uncertainty principle. Bohm showed it did not violate the uncertainty principle as I shall explain as I go along.
By assuming the Born probability postulate, the first equation corresponded to the conservation of probability. The form of the second equation had a strong resemblance to the classical Hamilton-Jacobi equation, if one assumed the classical canonical relation p = ∇S held when S was the phase of the wave function. This was a relation that Dirac uses and it was used later by Feynman2 in his ‘sum-over- paths’ approach. This second equation contains a term not present in the classical Hamilton-Jacobi equation. If one assumes the equation is still an expression for the conservation of energy, the term introduces a new quality of energy only present in quantum problems—the quantum potential energy.
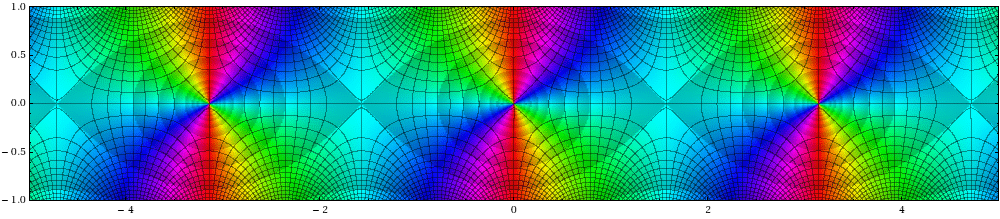
Although we have plenty of illustrations of how this energy accounted for all quantum behavior, very few wanted to seriously consider it as a physical entity in its own right. Its appearance was a mystery! Never mind, take it seriously and ask, ‘What role does it play in the new interpretation?’ To answer this question, consider the classic two-slit interference experiment where we see “particles” behaving like ‘waves.’ However, the solution of the second equation gives rise to an ensemble of possible trajectories the particles would take to produce the fringes. These trajectories were presented in a paper by Philippidis, Dewdney, and Hiley3 and are shown in Figure 1.
The trajectories to the right of the slits do not move in straight lines showing they must be subject to some force. That force has its origins in the quantum potential, shown in Figure 2 and this potential provides a straightforward explanation for the behavior of the particles.
However, for some reason that I have never been able to understand, this explanation was rejected and, instead, we are offered the notion of ‘wave- particle’ duality—particles behaving like waves and vice–versa, whatever that may mean. Bohr dresses all this up in a grand principle, the principle of complementarity. But this has always struck me as another example of the Hans Christian Andersen’s ‘The Emperor’s New Clothes.’
Of course, the emergence of this novel potential does not solve the mystery. We still have the problem of understanding the reason for the appearance of this extra term. In the last decade some physicists have started to propose answers to this question but we have had to wait a long time before people would even think about the problem. Of course, it requires thinking about quantum phenomena in a very different way from how we are taught.
It was the appearance of this new form of energy that David Peat focused on, showing it gave rise to subtle effects that could be used to explain more general experiences accessible to non-scientists4. How utterly sad to find that David Peat died shortly before the meeting he had planned took place. We will miss his contributions that have kept a more general interest in David Bohm’s work alive and relevant to today’s problems.
The question which faces physics here is why is it possible to get a seemingly simple explanation of quantum phenomena using the real and imaginary parts of the Schrödinger equation? How does this important and subtle quantum energy arise? But there is a deeper question, ‘Where does the Schrödinger equation itself come from in the first place?’ Why do I ask this? If you look into the history of quantum mechanics, you find that the early investigators like Heisenberg, Born, Jordan and Dirac were forced into proposing a new mathematical structure involving non-commutative objects. The physicists’ mathematics until then depended almost exclusively on commutative structures. Why should a technicality have such revolutionary consequences?
What does one mean by ‘commutative’ and ‘non-commutative’? In a commutative structure it does not matter in what order you take the symbols, for example 2+3 = 3+2, but in real life, order really does matter. Try walking through a door before opening it! The early quantum physicists learnt that order did matter. We have lost the importance of this fact because we think we are manipulating objects, whereas we should think about processes or activity. We focus on the wrong things, we focus on objects. But I would like to be provocative and remark objects are not important—they are a distraction. The success of the Schrödinger equation lulls us into believing order and action are unimportant, because by using the equation, the order appears not to matter. We have actually sneaked in the non-commutativity by writing the momentum as an operator and proceeding in the usual way.
For those who are not frightened by math, let me give a technical explanation. The time development equation for an operator A that Heisenberg came up with originally should be written in the form
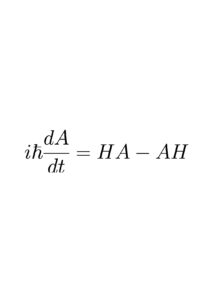
where H is the Hamiltonian, the energy of the system. There is a difference in the order HA and AH. This is a very different equation from the Schrödinger equation
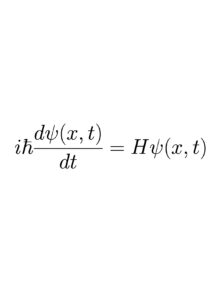
Here ψ(x, t) is the wave function defined by Aψ(x, t) = aψ(x, t), where a is the eigenvalue found by experiment when A is observed.
The common ground is in relation to eigenvalues, German for characteristic values, values that characterize the system. In the Heisenberg form they appear in the diagonal elements of a matrix. Since these elements appear in both approaches, they are assumed to be the mathematical objects that characterize the behavior of the particle—hence the name. But notice we have gone back to talking about objects, about particles. The eigenvalues actually characterize a process of activity, an activity that may continue for some time before being changed by a competing activity resulting in a change of the ongoing process. It is this process that lies at the heart of the Feynman sum over paths.
These possible characteristic processes can be in stacked in arrays of objects along the diagonal of a matrix. The magic of the matrix is that the position matrix cannot be made diagonal at the same time as the momentum matrix. This means we can characterize a process continually reoccurring at a point in space but we cannot simultaneously characterize the precise nature of its momentum and vice–versa. This is the mathematical way of capturing the Heisenberg uncertainty principle.
Heisenberg cemented its meaning by analyzing the process of examining a particle, an invariant of the process, under a microscope. Here there is a battle going on because as you try to make the position sharp, you make the momentum less sharp, and vice–versa. Attaching eigenvalues is then taken to be the only way to describe quantum ‘objects,’ because we are obsessed with objects. We try to make everything into an ‘object.’ A TV set is not of value because it is an object. It is of value because of its action in the process of bringing information in the form of news, entertainment etc. into our homes.
I hope the technical details do not frighten people off, but mathematics is a way of making general ideas more precise. It helps one to focus on what is important without being ‘lost in words.’ What David Bohm was very good at was interpreting the mathematical structure and conveying the ideas in such a way that the general audience can begin to grasp the meaning. Indeed, his ideas of the implicate-explicate order emerged from the fact that in a non-commutative structure not all the eigenvalues can be found at the same time; the set of eigenvalues distinguish each explicate order. That is really the idea lying behind the Heisenberg uncertainty principle. The eigenvalues of the operator corresponding to position cannot be specified if the eigenvalues of the momentum operator are specified. This means that if you know exactly where the particle is, you don’t know how fast it is going.

In our everyday experiences, we can find many examples of where we can specify some aspects of a subject, but other aspects become meaningless. We struggle to find words to describe the context in which we are working. Context is all-important in order to understand the meaning of some statement or process. Change the context and the process can become meaningless. David Bohm used a quote from Alice in Wonderland to illustrate this point. The March Hare’s watch was two days wrong. ‘I told you butter wouldn’t suit the works,’ was the Hatter’s angry reply. ‘It was the best butter,’ responded the Hare.
Another example occurs in gestalt psychology where a line drawing contains two different images such as the famous ‘flower vase or two faces,’ ‘antelopes or deer’ or the one I like to use, ‘old lady or young lady’ as shown in Figure 3. These examples show that two mutually independent and different representations can be encoded in the same image or structure. The mathematics of non-commutative structures is saying the same thing about fundamental material processes. This is totally unexpected from our understanding of classical physics, where it is assumed that we can say exactly where a car is and the speed it is travelling. But using the Schrödinger equation as a description of the time evolution of a particle does not allow you to do that. Yet, for example, the eigenvalues derived from the equation are the only way to explain the frequencies of light emitted from atoms.
Non-commutativity has a very general consequence, namely, that the whole of nature cannot be displayed before us with no enfolded or hidden aspects. This statement has huge ramifications for the way we order our life experiences. Moreover, this process of ordering is the source of all literature; fact and fiction tell the same story—there is no ultimate reality which we can rely on to guide us through life. Even the underlying reality of the material world is very different from the reality we give to objects in the macroscopic world which we experience daily. We have to make sense of a reality when we are trapped in a universe in which our experiences resemble the lessons we learn from gestalt psychology. What then is to replace the lines in the drawings used in our illustration of gestalt psychology? We have no images of the underlying reality and so what corresponds to the line drawing? Words with all their ambiguities or mathematics? Mathematics is what I use and I believe we must fully explore what it is telling us about this underlying reality. I am sorry but we cannot get away from the mathematics underpinning David Bohm’s beautiful ideas.
Development of Bohm’s Ideas
The aim of this section is to review Bohm’s earlier thinking about the conceptual problems presented by the quantum formalism and to explain how he overcame some of the difficulties he experienced in trying to understand Bohr’s position, the Copenhagen interpretation. I feel this discussion is needed because a great deal of confusion exists as to what exactly Bohm was striving towards when he first published his papers ‘A Suggested Interpretation of the Quantum Theory in Terms of Hidden Variables’5.
Many discussions about Bohm’s ideas in this area seem to concentrate on these two papers, assuming that they represented some kind of definitive and final theory which accurately reflects his later views. Bohm wrote these papers, not to present the definite alternative view of the quantum formalism, but merely to show that an alternative view, one that attributes definite properties to individual particles, was possible without radically changing the formalism and altering the predictions. I apologize for bringing back a concept that I would ultimately like to ban but, bear with me, I have to start with something familiar—but be prepared to give it up!
In chapter 4 of his book Causality and Chance in Modern Physics6, published in 1958, Bohm presented an appraisal of these earlier papers. On page 110, he writes

At this stage, as pointed out in Section 1, the author’s principal purpose had not been to propose a definitive new theory, but was rather mainly to show, with the aid of a concrete example, that alternative interpretations of the quantum theory were in fact possible. Indeed, the theory in its original form, although completely consistent in a logical way, had many aspects which seemed quite artificial and unsatisfactory. Nevertheless, as artificial as some of these aspects were, it did seem that the theory could serve as a useful starting-point for further developments, which it was hoped could modify and enrich it sufficiently to remove these unsatisfactory features.
Bohm’s own assessment of his early work seems to have been forgotten with the development of what is known as ‘Bohmian mechanics’ and, in consequence, the work he published in later papers refining and making new and at times revolutionary proposals becomes lost and completely ignored. In meeting some of his own earlier objections, Bohm found it necessary to make radical new proposals about the deeper structure underlying quantum phenomena. However, the seeds of what eventually emerged were already implicit, and sometimes even made explicit in his book Causality and Chance in Modern Physics7. It is the origins of these ideas that I want to discuss in this paper. Before doing, so I want to highlight some of the ideas developed by others that have been wrongly attributed to Bohm.
Non-Bohmian Mechanics
The misunderstandings gathered pace after the unfortunate appearance of the term ‘Bohmian Mechanics’ [BM], in a paper by Dürr, Goldstein and Zanghi [DGZ]8. The very term, ‘Bohmian Mechanics,’ lies at the root of much confusion concerning the direction that Bohm’s own thinking took after he first published his two seminal papers in 19529 *. While I quite understand the wish to give credit to Bohm for his pioneering work, the linking of Bohm’s name with the term ‘mechanics’ has led many to believe that Bohm himself was motivated to find a classical order based on an underlying deterministic mechanics from which the quantum formalism would emerge. That was never his intention.
Indeed, the content of his book Quantum Theory published in 195110, which gives an exhaustive account of the orthodox view of the theory, already sows the seeds of how radical a change Bohm thinks is needed in order to begin to understand the structure that underlies the quantum formalism. In that book he sees the need to go beyond mechanical ideas. In the section headed ‘The need for a non-mechanical description,’ he writes11,
*This remark should not be taken as a criticism of what Dürr et al.12 do in their paper. It is a perfectly legitimate and worthwhile enterprise to see how far a mechanical model will take us. Although this was not Bohm’s intention, his original papers13 left us with the problem of justifying the identification of the classical action with the phase of the wave function in the so called ‘guidance condition’ p = ∇S. Dürr et al. claimed to have derived this relation from first principles and thus removed this difficulty. Bohm’s proposal was that it should simply be taken as a ‘subsidiary14 until the emergence of a deeper theory.
…the entire universe must, on a very accurate level, be regarded as a single indivisible unit in which separate parts appear as idealizations permissible only on a classical level of accuracy of description. This means that the view of the world as being analogous to a huge machine, the predominant view from the sixteenth to nineteenth centuries, is now shown to be only approximately correct. The underlying structure of matter, however, is not mechanical.
In a footnote to this quote Bohm writes ‘This means that the term “quantum mechanics” is very much of a misnomer. It should, perhaps, be called “quantum non-mechanics.”’
It cannot be argued that this was just Bohm’s position before he published his 1952 papers because he takes up this ‘non-mechanics’ theme again in his book Causality and Chance in Modern Physics15 which was written later in 1956–7. This treatise was an attempt to put his ‘52 work in a more general context. Chapter 5 of this book contains a detailed criticism of the attempt to use classical mechanism in the quantum domain and could legitimately be subtitled ‘Against Mechanism.’ One does not even have to read the content to get a flavor of his arguments as the section headings speak for themselves. For example, section 3 is entitled ‘Criticism of the Philosophy of Mechanism,’ while section 4 reads ‘A Point of View that goes beyond Mechanism.’
Some Common Misapprehensions
One of the ideas that has been given prominence in the discussions of BM is the emphasis placed on the notion of a ‘particle,’ almost to the total exclusion of any wave-like properties. Thus, in many discussions, it is only the particle position and its momentum, defined by p = ∇S, that are given significance. The exclusive use of particle properties leads to many problems when applied to various experimental situations, which often lead to the conclusion that BM is actually ‘wrong.’ Yet how can a theory that uses the quantum formalism, without adding any new content, disagree with the predictions of the standard approach?16.
In many of these discussions, I find that there is no significance given to the quantum potential, yet for Bohm this was a key element in gaining insights into what could underlie the quantum formalism. In my many discussions with him, we developed the notion of a quantum potential which could be regarded as an ‘information’ potential, an internal potential that organized the form of the trajectories in a way that produced the behavior associated with quantum effects17.
Indeed, it was Bohm’s deeper analysis of this aspect of the approach that convinced him that the theory could not be mechanical. Rather it was ‘organic’ in the sense of Whitehead. Namely, that it was the whole that determined the properties of the individual particles and their relationship, not the other way round. For Bohm the universal interconnectedness of things could no longer be questioned and although this may be accepted even in the Newtonian paradigm, he felt this interconnectedness could not ultimately be reduced to nothing more than an interaction between some a priori given fundamental entities which compose the system18.
For Bohm there was no such thing as the fundamental particle, the ‘ultimon.’ At any stage of the analysis there are quasi-stable, semi-autonomous features that could be related, ordered and welded into a coherent structure which we could call a theory. However, these quasi-stable features, the ‘particles’ say, of the theory took their properties from the total process itself as we have discussed above.
We have the classic example of this type of feature in the appearance of phonons in a lattice of a solid. These phonons, although treated as the ‘particles’ of the theory, do not exist outside the lattice; they are the quanta of the thermal vibrations of the lattice. The lattice itself can be regarded as composed of much more stable particles, the atoms, but ultimately the atoms themselves could be thought of as quasi-stable, semi-autonomous entities of a deeper level, the quarks or yet more fundamental features of the underlying process. Of course, in many cases we can treat the atom as an entity independent of its background. This works for a large variety of processes until we come to effects like quantum interference. Are we right to continue to think of the atom in this situation as being independent of the experimental background in which we are examining its properties? Bohr clearly thought not when he referred to19.
the impossibility of any sharp separation between the behavior of atomic objects and the interaction with the measuring instruments which serve to define the conditions under which the phenomena appear.
Let us leave this question for the moment and return to the much maligned quantum potential. One of the assumptions behind BM is that the Schrödinger equation still holds. As indicated above what Bohm did initially was to examine the real and imaginary parts of this equation under polar decomposition of the wave function. This is a standard procedure in mathematics and, as is well known, this decomposition does not alter the content of the equation. It is in this decomposition that the real part of the Schrödinger equation is found to be
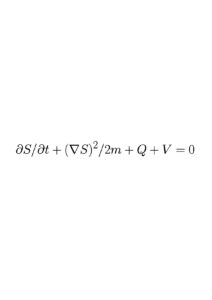
where Q is given the name ‘quantum potential.’ This clearly is a manifest feature of the equation and must surely have some physical consequences. Bohm took its appearance seriously and began to explore its significance in his original papers20.
Together, we continued this exploration, the details of which can be found in our review paper21, our book22 and, in more general terms, in the book of Bohm and Peat23. What we concluded was that this potential enabled the global properties of quantum phenomena to be focused on the particle aspect, but in doing this we must remember the ‘particle’ is not independent of the background. Furthermore, it is the quantum potential that contains the effects of this background. This implies that the particle and quantum potential form an indivisible whole, which for the sake of simplicity, we can call a ‘quantum blob’24. I will explain this feature in more detail later in this paper.
In the early Nineties I became aware of the work of DGZ (Dürr, Goldstein and Zanghi) after the manuscript of our book The Undivided Universe25 had been completed. On reading their paper ‘Bohmian Mechanics as the Foundation of Quantum Mechanics’26, I began to realize that DGZ were not discussing the ideas that Bohm himself had been developing but were proposing a significantly different theory. This soon becomes very apparent when they dismiss the quantum potential as not being ‘fundamental.’ But they actually say more. It is ‘ad hoc,’ ‘misleading,’ and ‘not natural.’ They emphatically reject its relevance by writing, ‘there is neither the need nor room for any further axioms involving the quantum potential’ 27.
Clearly BM is not the approach that Bohm originally proposed, nor is it the theory that our group at Birkbeck worked on with Bohm for three decades. I find the rejection of the quantum potential very puzzling, particularly in view of the beautiful work by de Gosson28 who shows that the quantum potential is an essential part of the mathematical structure that arises in symplectic geometry, a feature shared by both classical and quantum mechanics. Is the quantum potential ignored because it contains all the non-local features that are anathema to those who desire to hold onto a mechanistic interpretation? Or do people still cling to the logical positivists’ belief, long since discredited, that we must only talk about what is directly observable such as the particle position?
Bohm’s Motivation for his Original Proposals
Let us put aside the speculations about the motives of others and return to consider what Bohm was trying to achieve in his ‘52 papers. To make Bohm’s position absolutely clear, we must recall the background in which his proposals were put forward. The prevailing view at the time was that the only possible interpretation of the quantum formalism was Bohr’s Copenhagen interpretation. Von Neumann29 had shown, it was claimed, that there was no alternative. What von Neumann actually claimed was that it was not possible to find a deeper reality, usually associated with ‘hidden variables,’ underlying quantum phenomena without producing results that would disagree with those of the standard approach. Bohm had reached a similar conclusion in his own book30, but from very different arguments.
He explained to me that after the book was completed and on deeper reflection, he became dissatisfied with the argument and finally reached a different conclusion. He later writes31
What I felt especially unsatisfactory [with the conventional approach] was the fact that the quantum theory had no place in it for an adequate notion of an independent actuality.
Bohm insisted that his ‘52 papers should not be taken as his dramatic conversion to a deterministic, mechanical viewpoint. He was merely trying to show that an alternative that attributed properties to an underlying reality was possible. Bohm was not offering these proposals as the final definitive interpretation of the quantum formalism in the non-relativistic domain. There were too many curious features that needed careful thought. However, for starters, we could see how far we could go by assuming there was a definite localized entity that we could call a particle, to which we could attribute a precisely definable and continuously varying value for the position and the momentum together with the background energy Q. Bohm then shows that one can, indeed, obtain a consistent interpretation that would reproduce all the results of the standard formalism.
Throughout the papers Bohm stresses that his approach opens up possibilities of modifying the formalism in ways that could not be possible in the present formalism. For example, he suggested that there was a possibility of exploring deeper structures that could lie below 10−13cm. Clearly, he was not presenting the ideas as being, in some sense, a definitive interpretation of the formalism, but using them to look for something deeper.
In our conversations, Bohm said that he felt his early proposals were somewhat ad hoc and not totally convincing as a physically intelligible interpretation. Even Bell acknowledges that ‘Bohm did not like it very much’ 32. One can find many quotes from Bohm’s own papers over the years backing this claim. Even in our book, The Undivided Universe33, although we presented new ideas that answered some of the earlier criticisms, nowhere did we claim that our approach was entirely free of any difficulties. If we had thought it to be the ‘final’ theory, why did we devote the last chapter to describing a more radical approach?
Bohm’s Own Criticism of his Early Ideas
So what are the difficulties that Bohm, himself, perceived? These were set out in section 5 of chapter 4 of Causality and Chance in Modern Physics34.
Firstly, there was the question of how to extend these ideas to the spin of the electron. Bohm, together with Schiller and Tiomno35soon proposed a model based on the notion of a spinning top using the Cayley-Klein parameters and the Pauli equation. Although this has been investigated further by Dewdney, Holland and Kyprianidis36, it is not without its own difficulties. Some of these difficulties have been removed in a recent paper by Hiley and Callaghan37.
Secondly, although there have been attempts to extend these ideas to the relativistic electron, these have only been partially successful38, 39, 40, 41. Hiley and Callaghan42 have given a complete treatment of the relativistic Dirac electron in which the fully relativistic quantum potential is presented.
In the same section of his book, Bohm draws attention to what he calls ‘a serious problem’ that confronts us when the theory is extended to deal with more than one particle. The problem with N particles is that the wave function is not in ordinary three-dimensional space, but instead, in an abstract 3N-dimensional configuration space. While of course this space is logically consistent, the concept of a wave in a 3N-dimensional space is far from physically obvious. At this stage Bohm simply regarded his proposals as an artifice that could be used provisionally until a better theory emerged ‘in which everything is expressed once more in ordinary three-dimensional space,’ This problem of configuration space was eventually resolved by introducing the notion of ‘active information’43.
However there remains a deeper problem as Bohm points out44
Finally, our model in which wave and particle are regarded as basically different entities, which interact in a way that is not essential to their modes of being, does not seem very plausible. The fact that wave and particle are never found separately suggests instead that they are both different aspects of some fundamentally new kind of entity which is likely to be quite different from a simple wave or a simple particle, but which leads to these two limiting manifestations as approximations that are valid under appropriate conditions.
It is this problem that radically changes the meaning of the term ‘particle.’.
The Way Forward
In the last quotation of the previous section, we begin to see a germ of what was to lie ahead. The theory was not proposing the existence of a classical ‘rock-like’ particle, but rather a new kind of entity which is quite different from a classical particle. It is an entity that is a product of the interconnectivity of processes we see in nature. As we have remarked above, rather than think of interconnectivity as a product of the interaction of a priori given fundamental entities, it is the very interconnection that sustains the entities themselves, and defines their properties. Alter the background and the substructure of these interconnections and the entities themselves transform into new entities. His is not a world of immutable particles with well-defined properties interacting through mechanical forces. Something much more radical is involved. Bohm writes45
A fundamental problem in scientific research is then to find what are the things that in a given context, and in a given set of conditions, are able to influence other things without themselves being significantly changed in their basic qualities, properties, and laws. These are, then, the things that are, within the domain under consideration, autonomous in their essential characteristics to an adequate degree of approximation.
In the above Bohm talks about the ‘wave’ and the ‘particle.’ I would rather think of it in terms of energy, a localized kinetic energy and a global quantum potential energy. These are two manifestations of the same total interconnected process. Why do I say this?
Let us consider first two extreme situations. For the free particle, the total energy is all kinetic and there is no quantum potential energy. On the other hand, for a particle in a box in a stationary state, we find no kinetic energy and all the energy is in the quantum potential. In between these two extreme cases, we find the energy split between these two forms of energy. We find this division typically appearing in interference phenomena46. In these situations we find the quantum potential energy depends on some global aspect, such as, for example, the position and widths of the two slits in a two-slit interference experiment. In contrast to quantum phenomena, the classical behavior appears when all the energy is kinetic and the quantum potential energy vanishes. In this way the theory provides an explanation of why ‘particles’ behave differently in classical and quantum situations. What the theory does not tell us is why there is this schism in the energy in the first place. This is a question that a deeper theory must answer.
The Connection with Quantum Field Theory
Now let us turn to conventional quantum field theory [QFT]. Here it is the field that captures the global aspects of the phenomena. To describe the energy in QFT, we use the energy-momentum tensor, Tμν. If we consider the energy and momentum components, T00 and Tj0 of this tensor, we find they are exactly what we call the Bohm energy and Bohm momentum density. The details can be found in Hiley and Callaghan47 who show
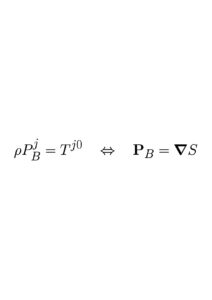
and that
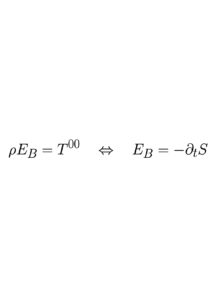
This generalizes to both the Pauli48 and Dirac49 cases. A similar result has also been found by Horton and Dewdney for the Klein-Gordon equation50, the scalar field51 and the massive vector field52.
Thus the Bohm energy and momentum appear to be part of standard QFT, so what are the essential differences between the two theories? QFT does not discuss the properties of Tμ0 itself. Rather it defines an energy- momentum Pμ via the equation
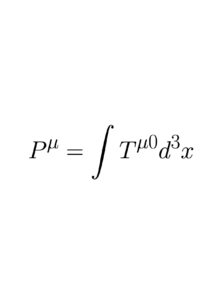
where the integral is taken over all space. In other words it defines a global energy-momentum and shows that this global energy is conserved.
On the other hand, Bohm considers the meaning of the local expression Tμ0(xρ) in the particular case when there is only one particle excitation present in the field. In other words, the energy is below the threshold for particle creation. Then one makes the assumption that we can attribute the value of the energy-momentum components Tμ0(xρ) to a quasi-local, semi- autonomous feature of the total energy. For convenience we can call this feature, the ‘particle.’ However, this ‘particle’ is different from a classical particle because it does not carry all the energy. Tij(xρ), remains to be accounted for. In the Bohm approach this energy is made manifest through the quantum potential and, as we have seen, it is this energy that is the source of all the quantum phenomena. This includes the quantum non-locality and quantum teleportation53, 54. Since standard QFT considers only the global properties, it cannot possibly reveal any of these non-local features.
Physicists are more familiar with the energy-momentum tensor, Tμν(xρ), when it arises in a fluid or in a crystal lattice. In these cases, the components Tij(xρ) are understood as the local energy involved in stresses and strains in the medium. What is puzzling about the notion of a ‘particle’ in the quantum domain is that it seems to be behaving like a quasi-stable feature in some medium. Indeed, this was a very early perception of some physicists and motivated the discussion of the possibility of a hydrodynamical model of quantum phenomena. These ideas, in fact, go back to the suggestions of Madelung55, which were used in a general theory by de Broglie56 and applied in a relativistic context of the Dirac equation by Takabayasi57.
Even Feynman58 uses the idea of a ‘fluid’ of electron pairs in his discussion of superconductivity. He derives, in fact, exactly the quantum Hamilton-Jacobi equation59 and calls the quantum potential, simply the ‘quantum mechanical energy.’ However in a footnote Feynman attributes the hydrodynamical ideas to Onsager, adding that ‘no one else ever understood why’ this should be the case. Is this just a happy coincidence or is it a reflection of something deeper that is involved?
Certainly, if we do not find more arguments to support the splitting of the internal energy between kinetic and quantum potential, we would be inclined to dismiss this whole structure as fanciful. However, there are two aspects of relativity that need to be remembered before coming to such a conclusion.
The first involves the difficulty that arises if we use the notion of a point particle in special relativity. Bohm argues that60
… it is not possible in relativity to obtain a consistent definition of an extended rigid body, because this would imply signals faster than light. …physicists were driven to the notion of a particle that is an extensionless point, but, as is well known, this effort has not led to generally satisfactory results because of the infinite fields implied by point particles. Actually, relativity implies neither the point particles nor quasi-rigid bodies can be primary concepts. Rather, these have to be expressed in terms of events and processes.
In other words, we have to move away from the idea that we can regard the particle as a quasi-rigid body with some extension. Standard theory avoids this difficulty by regarding the particle as an excitation of the field. But the field itself produces its own well-known singularities. For Bohm it is this particular difficulty that signaled the need to develop a radically new theory in terms of a discrete structure process61. He felt very strongly that the process philosophy that underlies these ideas should be accompanied by a change of mathematical emphasis, introducing what he called the ‘algebra of process’62. Bohm was never able to complete this work and it was only after his passing that I was able to show one possible way to carry out this program63.

The second aspect to which I want to draw attention is the unusual properties of the energy-momentum tensor of the gravitational field in general relativity. These properties are different from those of fields in flat space-time. One of the first surprises that attracted my attention was a discussion of the energy-momentum tensor of gravitational waves by Bondi64. It seems very timely that, at last, gravitational waves have been shown to exist. What clearly emerged from Bondi’s work was that energy was not localizable. This was taken further by Penrose who reached the conclusion that ‘energy is a genuinely non-local quantity’65.
It is very tempting to link the non-locality appearing in the gravitational energy with the quantum non-locality that manifests itself in the quantum potential. In fact, Penrose has already made reference to this possibility and has suggested that this is where his twistor program may help, although he feels more radically new ideas will ultimately be involved66, 67.
Now twistor theory emerges from the conformal Clifford algebra and Bohm and I have already shown how this structure may be used to discuss the Dirac electron68. But this paper was written in the context of a deeper process philosophy that Bohm felt offered a possible approach. Indeed already in the last chapter of Causality and Chance in Modern Physics69 in the section headed ‘The Process of Becoming’ he writes:
Thus far, we have been discussing the properties and qualities of things mainly in so far as they may be abstracted from the processes in which things are always changing their properties and qualities and becoming other things. We shall now consider in more detail the characteristics of these processes which may be denoted by ‘motion.’
The word ‘motion’ was later changed to ‘movement’ which, in turn, ultimately became the ‘holomovement’70. Here Bohm’s use of the notion of ‘movement’ is subtle. It is not the movement of objects, but is something more primitive and it is from this primitive movement that, not only objects, but space-time itself arises. Again, it is extremely exciting to see these ideas have not been developed in vain as has been recently shown in Rovelli71. One of the features that was missing in the early attempts to develop this more general approach was a mathematics in which to ground the ideas. Bohm had already set out a very clear rationale of the type of mathematics that he felt was worth exploring in his paper ‘Time, the Implicate Order and Pre-space’ published in 198672. There he writes
My attitude is that the mathematics of the quantum theory deals primarily with the structure of the implicate pre-space and with how an explicate order of space and time emerges from it, rather than with movements of physical entities, such as particles and fields. (This is an extension of what is done in general relativity, which deals primarily with geometry and only secondarily with the entities described within this geometry.)
I have been continuing this work and have recently written a paper discussing the technical aspects of what is involved in carrying out this exploration73. What I have shown is that by using the categorical notion of process captured by groupoids, one is led fairly naturally to Clifford algebras, the mathematics that is central to the Pauli and Dirac theories, as well as twistor theory. Indeed, I have shown how ‘shadow manifolds’ can be projected out of these algebras, thus constructing space-times as explicate orders of the deeper structure process which Bohm refers to as the implicate
Conclusion
I have argued here that Bohm’s ’52 papers74 were not an attempt to find a deterministic, mechanical account of the quantum formalism. He was well aware that if a clearer understanding of quantum phenomena was to be achieved, then we needed a radical new approach that would go deeper than the conventional view of what constitutes a quantum process. This deeper view would not take the notion of a particle as an a priori given structure. Rather the ‘particle’ would be some quasi-stable semi-autonomous feature of the unfolding process, taking its properties from the environment in which the movement is constrained. This gives a very different notion of a particle from that assumed in classical physics.
In the Sixties, when I had the privilege of working with Bohm, he was exploring many radical new ideas, and classical determinism could not have been further from his thoughts. Roger Penrose was at Birkbeck at that time and we had many discussions on how we could bring quantum mechanics and general relativity together in a single theory. Not surprisingly we reached different conclusions on how to proceed but what we did agree on was that a unification could not be achieved by sticking to the traditional view, namely, that physical processes can be adequately described in terms of particles/fields interacting in space-time. Rather there is a deeper underlying process from which not only do the particles and fields emerge, but this process is the source of space-time itself, an idea that is now gaining more general support.
Not surprisingly this idea is only just emerging, but what I wanted to do in this paper is to redress the view that prevails in much of the literature, namely, that Bohm was motivated by an overwhelming desire to return to a deterministic, mechanical world. The fact is that the main mathematical features of Bohm’s approach, the Bohm momentum PB = ∇S and the Bohm energy EB = −∂tS, have recently been shown to emerge more naturally from the low energy approximation of standard quantum field theory and these features are being tested experimentally by the group I am now working with at University College, London75, 76.
Acknowledgements
I would like to thank sincerely the people of Pari for their generous hospitality and support. A big thank you also to the Fetzer Franklin Foundation for their financial support that made my visit possible. I would also like to thank Glen Dennis for his careful and critical reading of the paper.
Notes
- Bohm, D., A Suggested Interpretation of the Quantum Theory in Terms of Hidden Variables, I, Phys. Rev., 85 (1952) 166-179; and II, 85 (1952) 180-193.
- Feynman, R. P., Space-time Approach to Non-Relativistic Quantum Mechanics, Rev. Mod. Phys. 20, (1948), 367-387.
- Philippidis, C., Dewdney, C. and Hiley, B. J., Quantum Interference and the Quantum Potential, Nuovo Cimento, 52B (1979) 15-28.
- Peat, F. D. (2008). Gentle Action: Bringing Creative Change to a Turbulent World. Pari, Italy: Pari Publishing Sas.
- Bohm, D., A Suggested Interpretation of the Quantum Theory in Terms of Hidden Variables, I, Phys. Rev., 85 (1952) 166-179; and II, 85 (1952) 180-193.
- Bohm, D. (1957). Causality and Chance in Modern Physics. London: Routledge & Kegan Paul
- Ibid
- Dürr, D., Goldstein, S. and Zanghi, N., Quantum Equilibrium and the Origin of Absolute Uncertainty, J. Stat. Phys., 67 (1992) 843-907.
- Bohm, D., A Suggested Interpretation of the Quantum Theory in Terms of Hidden Variables, I, Phys. Rev., 85 (1952) 166-179; and II, 85 (1952) 180-193.
- Bohm, D. (1951). Quantum Theory. Englewood Cliffs, N.J.: Prentice-Hall, p. 167.
- Ibid, p. 167.
- Dürr, D., Goldstein, S. and Zanghi, N., Quantum Equilibrium and the Origin of Absolute Uncertainty, J. Stat. Phys., 67 (1992) 843-907.
- Bohm, D., A Suggested Interpretation of the Quantum Theory in Terms of Hidden Variables, I, Phys. Rev., 85 (1952) 166-179; and II, 85 (1952) 180-193.
- Bohm, D., Comments on a Letter Concerning the Causal Interpretation of Quantum Theory, Phys. Rev., 89 (1953) 319-20.
- Bohm, D. (1957). Causality and Chance in Modern Physics. London: Routledge & Kegan Paul.
- Bedard, K., Material Objects in Bohm’s Interpretation, Phil. Sci., 66 (1999) 221-242.
- Bohm, D. and Hiley, B. J., An Ontological Basis for Quantum Theory: I – Non-relativistic Particle Systems, Phys. Reports, 144 (1987) 323-348.
- Bohm, D. (1957). Causality and Chance in Modern Physics. London: Routledge & Kegan Paul, pp. 143-4.
- Bohr, N. (1961). Atomic Physics and Human Knowledge. New York: Science Editions, pp. 39-40.
- Bohm, D., A Suggested Interpretation of the Quantum Theory in Terms of Hidden Variables, I, Phys. Rev., 85 (1952) 166-179; and II, 85 (1952) 180-193.
- Bohm, D. and Hiley, B. J., An Ontological Basis for Quantum Theory: I – Non-relativistic Particle Systems, Phys. Reports, 144 (1987) 323-348.
- Bohm, D. and Hiley, B. J. (1993). The Undivided Universe: An Ontological Interpretation of Quantum Theory. London: Routledge.
- Bohm, D. and Peat, D. F. (1987). Science, Order, and Creativity. New York: Bantam, pp. 180-184.
- de Gosson, M. A., Symplectically covariant Schrödinger equation in phase space J. Phys. A: Math. Gen., 38 (2005) 92639287.
- Bohm, D. and Hiley, B. J. (1993). The Undivided Universe: An Ontological Interpretation of Quantum Theory. London: Routledge.
- Dürr, D., Goldstein, S. and Zanghi, N., Bohmian Mechanics as the Foundation of Quantum Mechanics, in Bohmian Mechanics and Quantum Theory: An Appraisal. (1996), ed. Cushing, J. T., Fine, A. and Goldstein, S., Boston Studies in the Philosophy of Science, 184, Dordrecht: Kluwer, p. 26
- Ibid, p. 25.
- de Gosson, M., The quantum motion of half-densities and the derivation of Schrödinger’s equation, J. Phys. A: Math. Gen., 31 (1998) 4239-4247.
- von Neumann, J. (1955). Mathematical Foundations of Quantum Mechanics. Princeton: Princeton University Press.
- Bohm, D. (1951). Quantum Theory. Englewood Cliffs, N.J., p. 167.
- Hiley, B. J. and Peat, D. F. (1987). Quantum Implications: Essays in Honour of David Bohm. London: Routledge, Chapter 2.
- Bell, J. S. (1987). Speakable and Unspeakable in Quantum Mechanics. Cambridge: Cambridge University Press, p. 163.
- Bohm, D. and Hiley, B. J. (1993). The Undivided Universe: An Ontological Interpretation of Quantum Theory. London: Routledge.
- Bohm, D. (1957). Causality and Chance in Modern Physics. London: Routledge & Kegan Paul.
- Bohm, D., Schiller, R. and Tiomno, J., A Causal Interpretation of the Pauli Equation (A) and (B), Nuovo Cim. Supp. 1 (1955) 48-66 and 67-91.
- Dewdney, C., Holland, P. R. and Kyprianidis, A., What happens in a spin measurement? Phys. Letts. A, 119 (1986) 259-67.
- Hiley, B. J. and Callaghan, R. E., The Clifford Algebra approach to Quantum Mechanics A: The Schr ̈odinger and Pauli Particles, preprint 2010.
- Bohm, D. and Hiley, B. J. (1993). The Undivided Universe: An Ontological Interpretation of Quantum Theory. London: Routledge.
- Bohm, D., Classical and Non-Classical Concepts in the Quantum Theory, British J. Phil. Sci., XII (1962) 265-280.
- Hestenes, D., Space-time physics with geometric algebra, Am. J. Phys., 71 (2003) 691-714.
- Doran, C. and Lasenby, A. (2003). Geometric algebra for physicists. Cambridge: Cambridge University Press.
- Hiley, B. J. and Callaghan, R. E., The Clifford Algebra Approach to Quantum Mechanics B: The Dirac Particle and its relation to the Bohm Approach, preprint 2010.
- Bohm, D. and Hiley, B. J., An Ontological Basis for Quantum Theory: I – Non-relativistic Particle Systems, Phys. Reports, 144 (1987) 323-348.
- Bohm, D. (1957). Causality and Chance in Modern Physics. London: Routledge & Kegan Paul, p. 117.
- Ibid, p. 145.
- Philippidis, C., Dewdney, C. and Hiley, B. J., Quantum Interference and the Quantum Potential, Nuovo Cimento, 52B (1979) 15-28.
- Hiley, B. J. and Callaghan, R. E., The Clifford Algebra approach to Quantum Mechanics A: The Schrödinger and Pauli Particles, preprint 2010
- Ibid
- Hiley, B. J. and Callaghan, R. E., The Clifford Algebra Approach to Quantum Mechanics B: The Dirac Particle and its relation to the Bohm Approach, preprint 2010.
- Horton, G. and Dewdney, C., A Non-local, Lorentz-invariant, Hidden- variable Interpretation of Relativistic Quantum Mechanics, J. Phys. A: Math. Gen., 34 (2001) 9871-9878.
- Horton, G. and Dewdney, C., A relativistically covariant version of Bohm’s quantum field theory for the scalar field, J. Phys. A: Math. Gen., 37 (2002) 11935-11943.
- Horton, G. and Dewdney, C., Energy momentum flows for the massive vector field, quant-ph/0609198.
- Bohm, D. and Hiley, B. J., On the Intuitive Understanding of Nonlocality as Implied by Quantum Theory, Found. Phys., 5 (1975) 93-109.
- Maroney, O. and Hiley, B. J., Quantum State Teleportation understood through the Bohm Interpretation, Found. Phys., 29 (1999) 1403-15.
- Madelung, E., Quantentheorie in hydrodynamischer Form, Zeit. f. Phys., 40 (1926) 332, DOI: 10.1007/BF01400372.
- de Broglie, L., The Reinterpretation of Wave Mechanics, Found. Phys., 1 (1970) 5-15.
- Takabayasi, T., Relativistic Hydrodynamics of Dirac Matter, Prog. Theor. Phys. Supp., 4 (1957) 2-80.
- Feynman, R. P., Leighton, R. B. and Sands, M., The Feynman Lectures on Physics III, p. 21-12, Addison-Wesley, Reading, Mass, 1965.[41] Bohm, D. (1980). Wholeness and the Implicate Order. London: Routledge, pp. 123-4.
- Feynman, R. P., Space-time Approach to Non-Relativistic Quantum Mechanics, Rev. Mod. Phys. 20, (1948), 367-387.
- Bohm, D. (1980). Wholeness and the Implicate Order. London: Routledge, pp. 123-4.
- Bohm, D., Space, Time, and the Quantum Theory Understood in Terms of Discrete Structural Process, Proc. Int. Conf. on Elementary Particles, Kyoto, (1965), 252-287.
- Bohm, D., Time, the Implicate Order and Pre-Space, in Physics and the Ultimate Significance of Time, ed. D. R. Griffin, pp. 172-6 & pp. 177-208, SUNY Press, N.Y., (1986).
- Hiley, B. J., Process, Distinction, Groupoids and Clifford Algebras: an Alternative View of the Quantum Formalism, Coecke, B., Lecture Notes in Physics, vol. 813, pp. 705-750, Springer (2011). arXiv: 1211.2098.
- Bondi, H., Gravitational waves in General Relativity, Nature, 186, (1960) 535.
- Penrose, R. (2004). The Road to Reality. London: Jonathan Cape, Section 19.8.
- Penrose, R., Quasi-local mass and angular momentum in general relativity, Proc. R. Soc. Lond., A381 (1982) 53-63
- Penrose, R. (1990). The Emperor’s New Mind. London: Vintage, p. 480.
- Bohm, D. and Hiley, B. J., Generalization of the Twistor to Clifford Algebras as a basis for Geometry, Rev. Brasileira de Fisica, Volume Especial, Os 70 anos de Mario Sch ̈onberg, (1984) 1-26.
- Bohm, D. (1957). Causality and Chance in Modern Physics. London: Routledge & Kegan Paul, pp.146-7.
- Bohm, D., Hiley, B. J. and Stuart, A. E. G., On a New Mode of Description in Physics, Int. J. Theor. Phys., 3 (1970) 171-183.
- Rovelli, C. (2004). Quantum Gravity. Cambridge: Cambridge University Press
- Bohm, D. (1986). Time, the Implicate Order and Pre-Space, in Physics and the Ultimate Significance of Time, ed. D. R. Griffin. New York: SUNY Press. pp. 172-6 & pp. 177-208.
- Hiley, B. J., Process, Distinction, Groupoids and Clifford Algebras: an Alternative View of the Quantum Formalism, Coecke, B., Lecture Notes in Physics, vol. 813, pp. 705-750, Springer (2011). arXiv: 1211.2098.
- Bohm, D., A Suggested Interpretation of the Quantum Theory in Terms of Hidden Variables, I, Phys. Rev., 85 (1952) 166-179; and II, 85 (1952) 180-193.
- Morley, J., Edmunds, P. D. and Barker, P. F., Measuring the weak value of the momentum in a double slit interferometer, J. Phys. Conference series 701 (2016) 012030.
- Monachello, V., Flack, R., Hiley, B. J. and Callaghan, R. E., A method for measuring the real part of the weak value of spin using non-zero mass particles, arXiv:1701.04808.


